TDMR Channel Model
TDMR channels achieve high recording densities by reducing the size of bits to the order of size of the magnetic grains on the medium. The effects of the random distribution of grains on the medium becomes more pronounced, resulting in the jitter noise. At low recording densities, the jitter noise can be modeled as a first order variation of the channel response. At high recording densities, a mode accurate channel model including the randomness in the grain positions has to be used. In bit-patterned media (BPM), the jitter noise is not observed due to regular ordering of the grains on the medium

Figure 1: Position of grains on magnetic medium is modeled using Poisson point process with “boundary sampling” – each new grain is randomly generated such that it touches at least one of the existing grains.
The position of the grains on the TDMR medium can be modeled as a Poisson point (dart-throwing) process with a constrains on the minimum and maximum distance between the grains. The region of maximal influence of each grain is the Voronoi region containing the grain center. The medium is split in to a rectangular grid where each rectangular cell corresponds to a channel bit. During write process, all grains lying in a bit-position are magnetized to the same polarity depending on the bit value. During read process, each grain contributes to a signal given by the read-head sensitivity function that depends on the geometry and positioning of the read head. The read back signal is the summation of contributions from all grains on the medium. The read-head sensitivity function is modeled as a 2D Gaussian pulse, extending the Gaussian pulse model of the 1D perpendicular magnetic recording. A simulated distribution of grains, magnetization of the corresponding Voronoi regions and the read-back signal are shown in Figures 1,2 and 3.
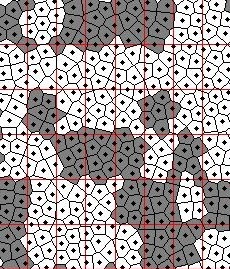
Figure 2: The region of maximum influence of each grain is represented as a Voronoi cell. The rectangular grid indicates the bit boundaries. All grains within a bit-boundary have the same magnetic polarization. The magnetic domains are formed by the collection of neighboring Voronoi cells with same magnetic polarization. The jitter noise is the result of the a) irregular boundaries of the magnetic domains and b) the variation in the number of grains per bit.

Figure 3: The read-back signal for the simulated medium is shown. The contribution from each grain is given by read-head sensitivity function. The sensitivity function is modeled as a 2D Gaussian pulse.
Relevant topics: Signal modeling, point processes.
2D Error correcting codes
In TDMR, the data is structured as 2D blocks irrespective of the native format of the data. Each 2D block data is encoded using a 2D error correcting code and a modulation code resulting in a 2D block of data. 2D modulation codes help in mitigating excess ISI and other channel impairments, thereby, facilitating signal processing. The error correcting codes must be able to identify and correct random errors and 2D bursts arising from defects as well as scratches on the surface of the medium. Constructing two and higher dimensional ECCs and modulation codes are timely and important as technologies evolve from a 1D paradigm towards higher dimensions such as TDMR, 3D flash etc.
In the area of multi-dimensional modulation codes, the combinatorial capacities of many constrained channels are unknown, barring bounds known in a few cases. We need a general theory for determining the capacity of constrained channels and designing rate efficient codes. The tools involve probability theory, combinatorics and dynamical systems.
Error detection and correction in two and higher dimensions is significantly difficult than in 1D. Unlike a string of burst or random errors in 1D, the shapes in higher dimensions, clusters and related statistics play an important role in constructing efficient codes. Algebra in two-dimensions involves bivariate polynomials over fields, thereby, requiring advanced concepts on error ideals and such as opposed to straightforward techniques in 1D.
![]()
Figure 4(a): This 1D code structure is horizontally oriented, which means the burst will only have one shape that is horizontal.
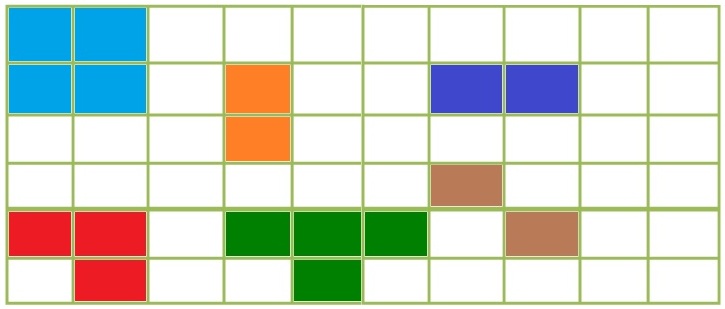
Figure 4(b): A 2D received code word can contain burst errors in many shapes as shown in colored font.
Relevant topics: The tools involve algebra (both linear and Galois), probability theory and combinatorics.
Team members
- Prof. Shayan G. Srinivasa (Chief Investigator)
- Chaitanya Kumar Matcha (Ph.D. student)
- Shounak Roy (Ph.D. student)
- Arjit Mondal (Ph.D. student)
- Arnab Dey (M.E. student)
- Saugata Datta (M.E. student)
- Sebin Jose (M.E. student)
- Arathy B Nair (Project Assistant)
Sponsor
- Department of Electronics and Information Technology (DeitY), India.
Collaborator / Co-Investigator
- Prof. Navin Kashyap, ECE, IISc
Publications
- S. Roy, A. Mondal and S. S. Garani, “A Fast and Efficient Two-Dimensional Chien Search Algorithm and Design Architecture”, IEEE. Comm. Letters, vol. 23, no. 1, pp. 16-19, Jan. 2019.
- A. B. Nair, A. Mondal and S. S. Garani, “A Low-complexity Hardware AWGN Channel Emulator on FPGA using Central Limit Theorem” in IEEE Int. Midwest Symp. on Circuits and Syst, Windsor, Canada, Aug. 2018.
- S. Roy, S. S. Garani, “Two dimensional algebraic error correcting codes”, ITA, Feb. 2018.
- A. Mondal, S. Thatimattala, V. K. Yalamaddi and S. S. Garani, “Efficient Coding Architectures for Reed-Solomon and Low-Density Parity-Check Decoders for Magnetic and Other Data Storage Systems,” in IEEE. Trans. Magn., vol. 54, no. 2, pp. 1-15, Feb. 2018.
- A. Dey, S. Jose, K. Varghese and S. G. Srinivasa, “A High-Throughput Clock-less Architecture for Soft-Output Viterbi Detection”, in IEEE International Midwest Symposium on Circuits and Systems, Boston, USA, Aug. 2017.
- C. K. Matcha, M. Bahrami, S. Roy, S. G. Srinivasa and B. Vasic, “Generalized Belief Propagation Based TDMR Detector and Decoder,” in IEEE. Proc. Intl. Symp. Inform. Theory,Barcelona, Spain, July 2016.
- S. Datta, K. Varghese and S. G. Srinivasa, ”A Non-uniformly Quantized High Throughput Soft Output Viterbi Detector on FPGA,” in IEEE Proc. VLSI, Kolkata, India, Jan. 2016.
- S. Datta and S. S. Garani, “Design Architecture of a Two-Dimensional Separable Iterative Soft Output Viterbi Detector,” in IEEE. Trans. Magn., vol.52, no. 1, Jan. 2016.
- S. Roy and S. G. Srinivasa, “Two Dimensional Error-Correcting Codes using Finite Field Fourier Transform”, in IEEE Inf. Theory Work., ITW, Jeju Island, Oct. 2015.
- C. K. Matcha and S. G. Srinivasa, “Generalized Partial Response Equalization and Data-Dependent Noise Predictive Signal Detection Over Media Models for TDMR,” in IEEE. Trans. Magn., vol. 51, no.10, pp.1-15, Oct. 2015.
- C. K. Matcha and S. G. Srinivasa, “Exact Analysis of the Performance of Viterbi Detector for ISI Channels with Quantized Inputs,” in IEEE. National Conf. On Comm. (NCC), Mumbai, India, Mar. 2015.