2D Timing Recovery
Timing recovery is essential at the front end of the read channel to facilitate signal detection. The timing recovery module estimates and corrects the timing and position errors in the read samples. We have developed two architectures for timing recovery in TDMR channels. One architecture uses a 2D phase-locked loop (PLL) for jointly estimating timing and position errors in X and Y directions. The other architecture uses two coupled 1D PLLs that act separately on X and Y directions. While the 2D PLL based method achieves better performance, the 1D PLL based design is simpler for implementation. We have proved the convergence of the algorithms analytically.
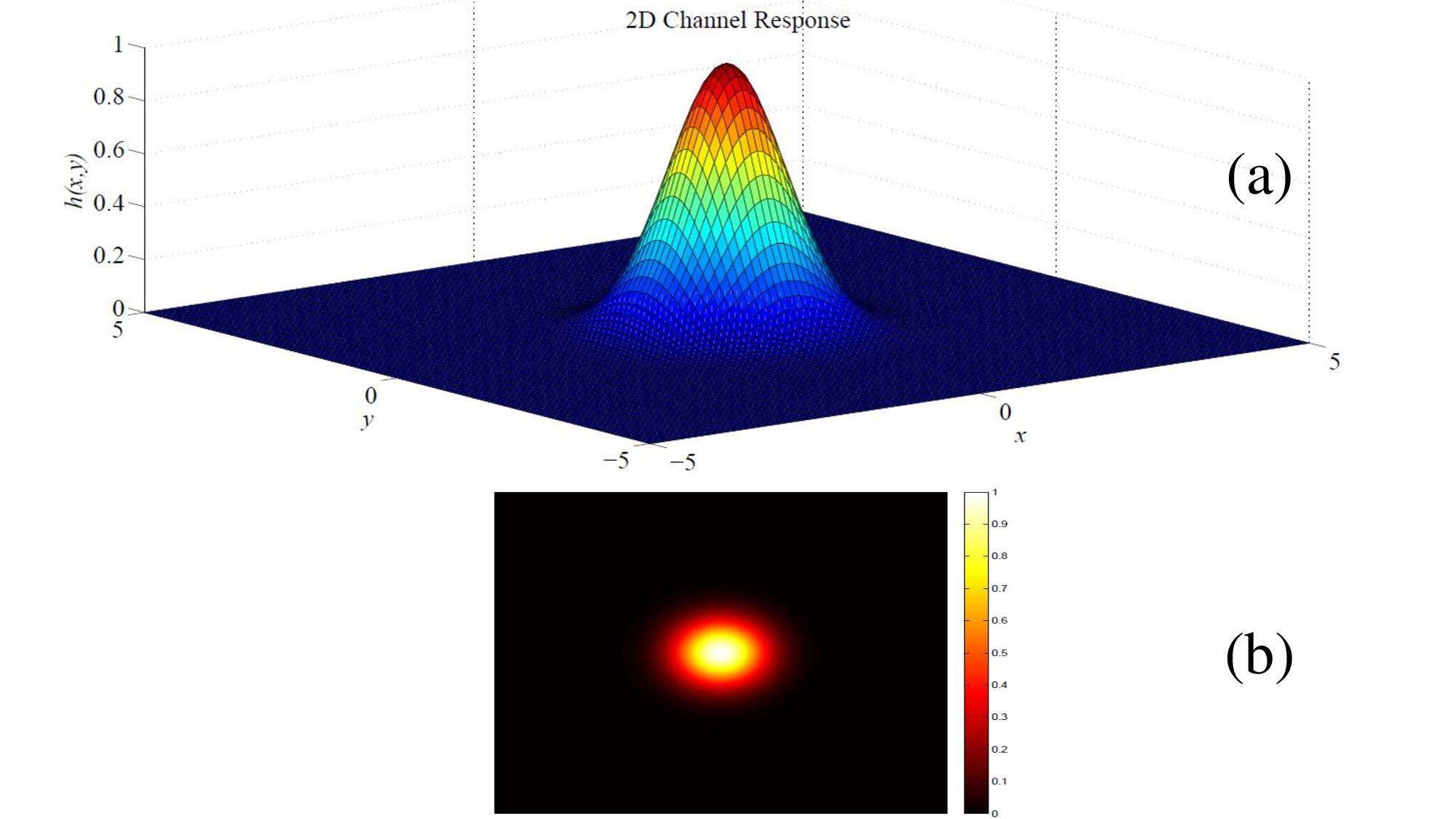
Figure 1: The impulse response of a 2D magnetic read head with an oversampling ratio of 100, wx = 1:0, wy = 1:0, a = 1
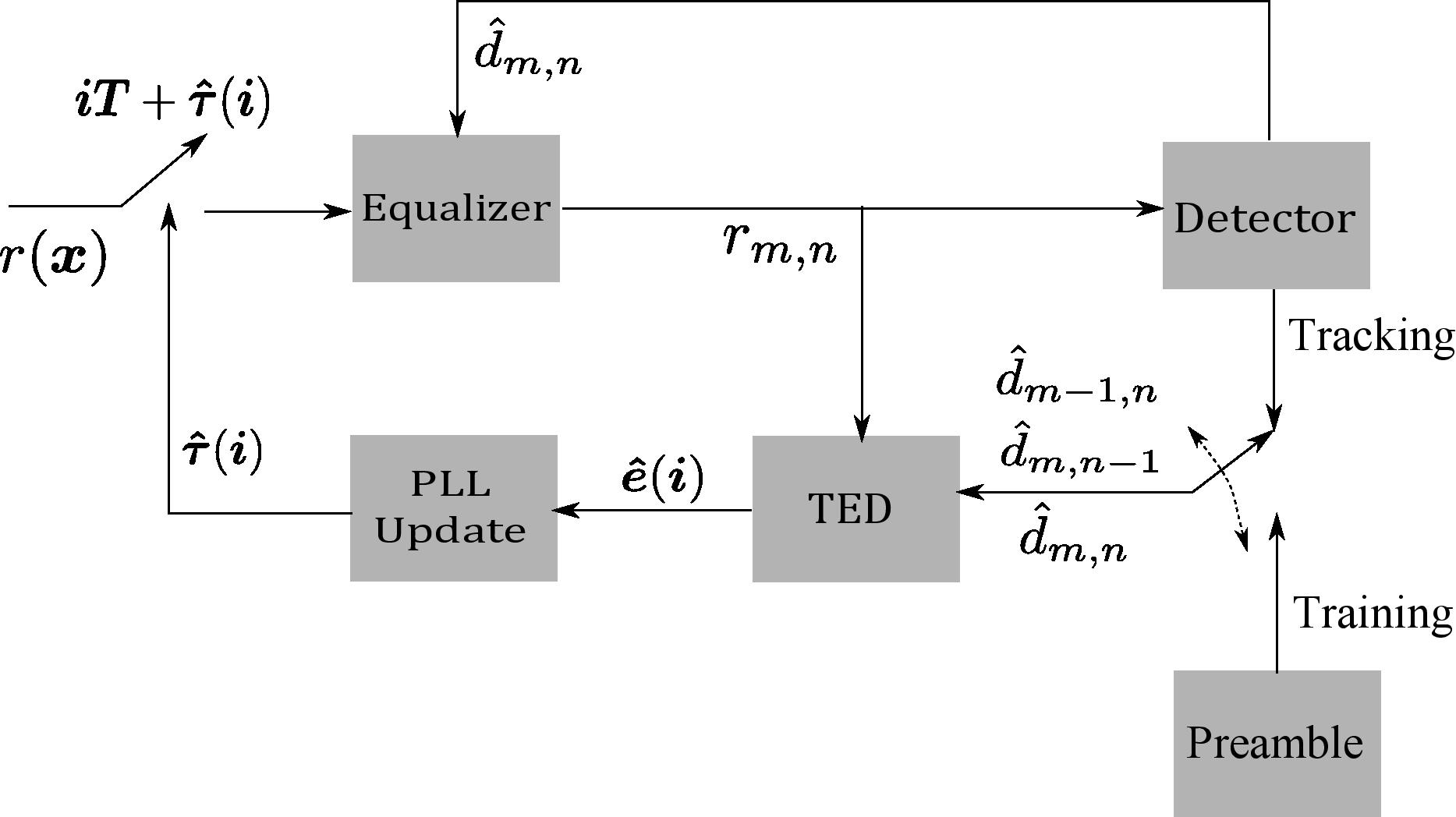
Figure 2: Architecture of the 2D PLL. The timing estimates τ̂(i) are used to correct the sampling instants at iTT.
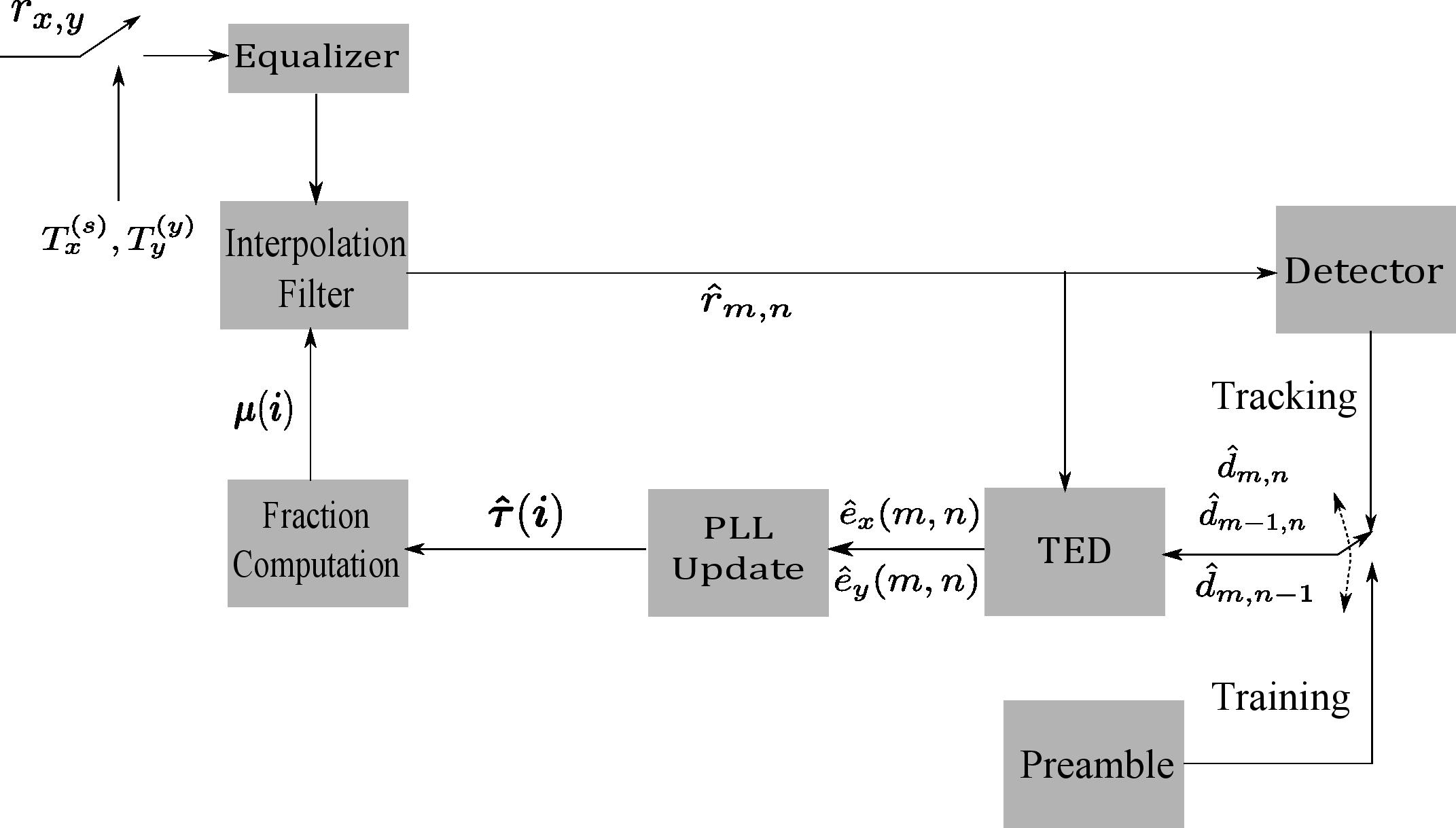
Figure 3: Schematic architecture of the ITR scheme.
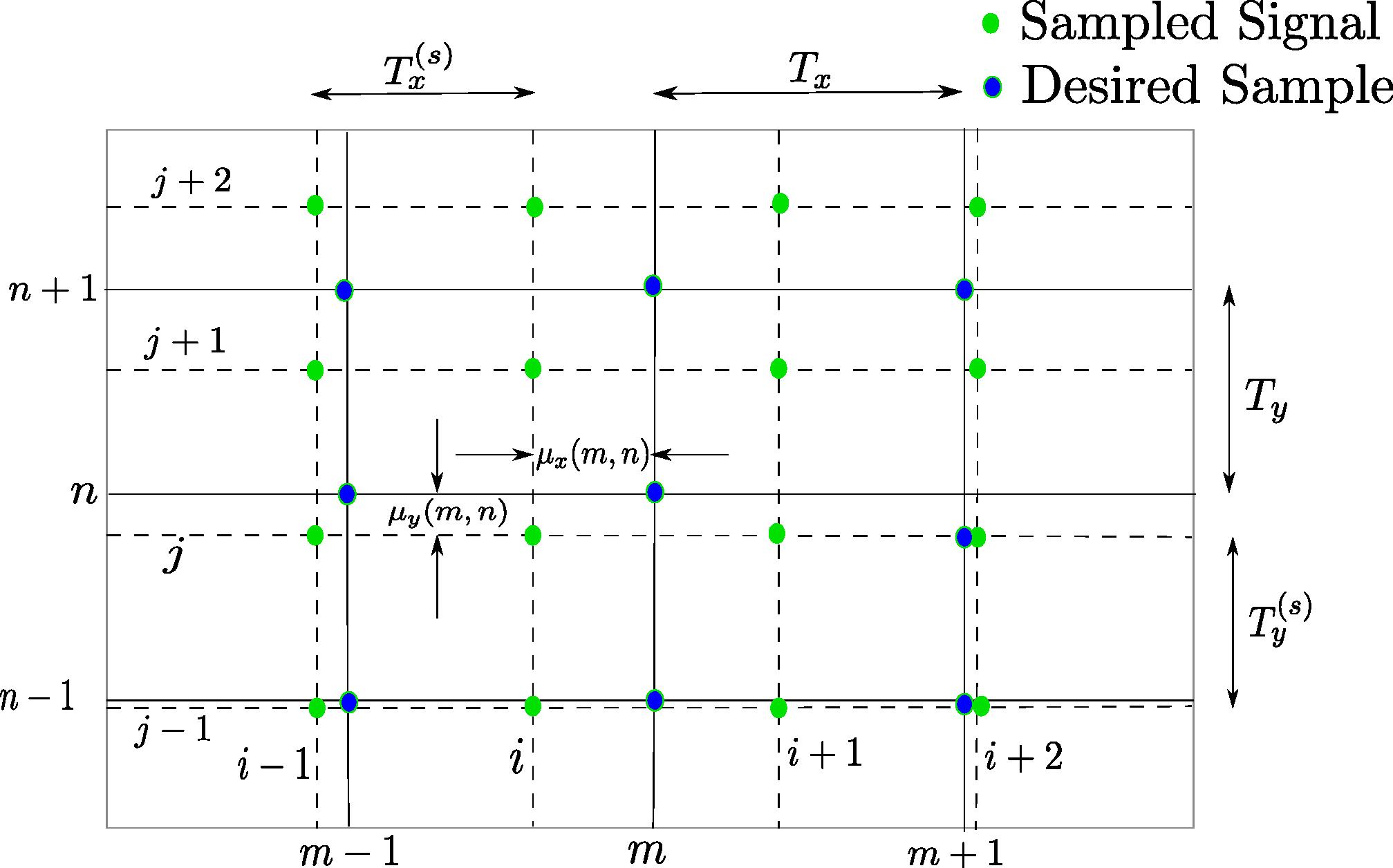
Figure 4: The sampled points of the read back signal jTTs and the desired samples are at the intersections of the dotted and solid lines. The interpolation filter attempts to estimate the samples at the desired points from the sampled signal.
Relevant topics: Phase locked loops, interpolated timing recovery, detection and estimation theory.
2D Signal Detection
TDMR requires sophisticated signal detection algorithms to mitigate the 2D ISI. The bit and grain sizes are comparable in TDMR channels and hence poses an additional challenge to mitigate the jitter noise due to irregularity in the grain positions. This jitter noise dominates the electronic noise as the bit density increases. The theoretical challenges for signal detection are multi-fold.
The maximum likelihood (ML)/maximum a-posteriori (MAP) detection is NP-hard for 2D ISI and the estimation of the capacity of 2D ISI channels for binary alphabet is non-trivial. Capacity achieving algorithms as well as near-optimal low-complexity detection algorithms are of research interest. The known detection methods include a) linear equalization followed by 1D ML detection, b) iterative detection using row-column detectors, c) low-complexity algorithms tuned for separable channel response and d) generalized belief propagation (GBP) using probabilistic graphical model. Among these, Joint 2D equalization and detection (JTED) is the only known algorithm shown to achieve MAP performance iteratively.
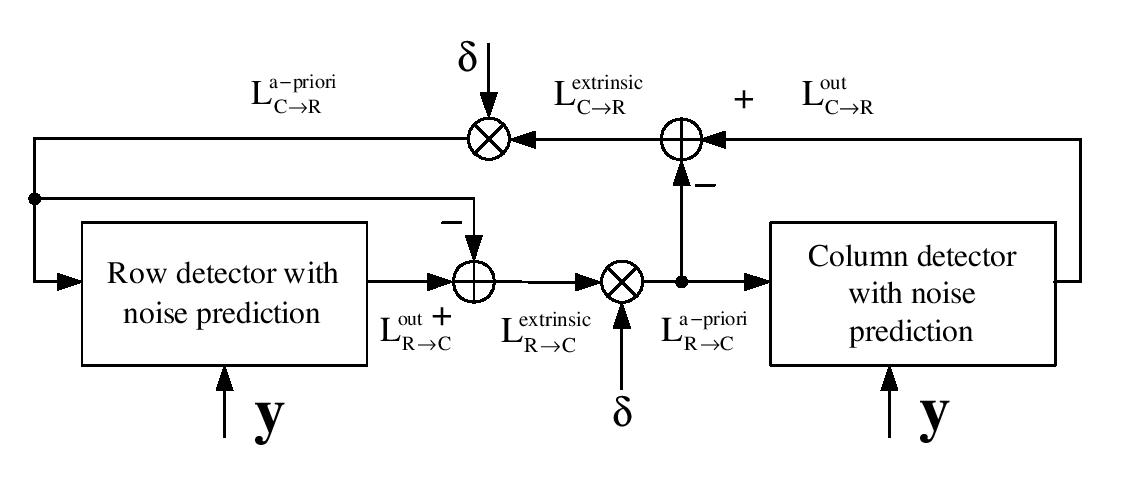
Figure 5: Schematic of the 2-D iterative multi-row/column feedback based detector (TIMRCFD).
We have proposed a low-complexity detection algorithm as an approximation to ML criterion using the ideas from 1D Viterbi algorithm. We have also extended the partial response maximum likelihood detection (PRML) scheme from 1D to 2D paradigm and proposed methods to design 2D partial response targets. We have also extended the data dependent noise prediction (DDNP) algorithm to mitigate the jitter noise for a Voronoi based channel model.

Figure 6: A low-complexity 2D extension of the 1D Viterbi algorithm. The algorithm makes decisions in the raster scan order by minimizing ML metric (to maximize the ML probability) of the read samples in a local neighborhood. The figure shows the decision order and local span of symbols used for a 3×3 ISI mask and a 3×3 local span for computing the ML metric.
The the jitter noise also imposes constraints on the data patterns that can be written on the medium and hence constrained coding is essential for TDMR channels. The construction and capacity estimation of the constrained codes is not trivial. Very few 2D constraint codes have a closed form expression for the capacity. The code construction and capacity estimation uses methods from the tessellation, combinatorics and statistical mechanics.
Relevant topics: probability, Markov chains, information theory, detection and estimation theory, tessellation, combinatorics, statistical mechanics.
Team members
- Prof. Shayan G. Srinivasa (Chief Investigator)
- Chaitanya Kumar Matcha (Ph.D. student)
- Eeshan Modak (Research assistant)
Sponsor
- Department of Science and Technology (DST), India. Grant no. SERB/F/3371/2013-14.
Publications
- S. S. Garani, L. Dolecek, J. Barry, F. Sala and B. Vasic, “Signal Processing and Coding Techniques for 2-D Magnetic Recording: An Overview”, in Proc. of the IEEE., vol. 106, no. 2, pp. 286-318, Feb. 2018.
- C. K. Matcha and S. S. Garani, “Joint Timing Recovery and Signal Detection for Two-Dimensional Magnetic Recording,” IEEE. Trans. Magn., vol. 53, no. 2, Feb. 2017.
- C. K. Matcha and S. S. Garani, “Defect Detection and Burst Erasure Correction for TDMR,” in IEEE. Trans. Magn., vol. 52, no. 11, Nov. 2016.
- E. Modak, B. Reddy and S. G. Srinivasa, ”Optimum Timing Interpolation Algorithm for 2-D Magnetic Recording Systems” in IEEE Natl. Conf. Comm., Guwahati, India, Mar. 2016.
- M. Bahrami, C. K. Matcha, S. M. Khatami, S. Roy, S. G. Srinivasa and B. Vasic, “Investigation into Harmful Patterns over Multi-Track Shingled Magnetic Detection Using the Voronoi Model,” in IEEE. Trans. Magn. vol. no. 99, pp.1-8, July 2015.
- C. K. Matcha and S. G. Srinivasa, “A Study on the Implications of Grain Density Distribution over the Granular Media Model for TDMR,” in IEEE. Intl. Conf. on Magnetics (Intermag), Beijing, China, May 2015. (In review for publication in IEEE. Trans. Magn.)
- B. P. Reddy, S. G. Srinivasa, and S. Dahandeh “Timing recovery algorithms and architectures for two-dimensional magnetic recording systems,” To appear IEEE. Trans. Magn., Mar. 2015.
- C. K. Matcha and S. G. Srinivasa, “Target design and low complexity signal detection for two dimensional magnetic recording,” in IEEE. Asia-Pacific Signal and Inform. Proc. Conf., Siem Reap, city of Angkor Wat, Cambodia, Dec. 2014.
- B. P. Reddy, S. G. Srinivasa and S. Dahandeh, “Timing Recovery Algorithms and Architectures for Two-Dimensional Magnetic Recording Systems,” in IEEE. Magn. Record. Conf., Berkeley, Aug. 2014.
- C. K. Matcha, S. G. Srinivasa, S. M. Khatami and B. Vasic, “Two-dimensional noise-predictive maximum likelihood method for magnetic recording channels,” in IEEE. Intl. Symp. Inform. Theory and Appl., Melbourne, Oct. 2014.
- B. P. Reddy and S. G. Srinivasa, “Two-dimensional signal processing for timing recovery using PLLs for storage channels,” in IEEE. China Summit and Intl. Conf. Signal and Inform. Processing, Xi’an, July 2014.
- Y. Chen and S. G. Srinivasa “Joint self-iterating equalization and detection for two-dimensional intersymbol-interference channels,” IEEE. Trans. Comm., vol. 61, no. 8, pp. 3219-3230, Aug. 2013.
- Y. Chen and S. G. Srinivasa, “Performance-Complexity trade-offs of the 2-D iterative feedback signal detection algorithm,” in IEEE. Intl . Conf. Computing, Networking and Communications, San Diego, Jan. 2013.
- Y. Chen and S. G. Srinivasa, “Signal detection algorithms for two-dimensional intersymbol-interference channels,” in IEEE. Proc. Intl. Symp. Inform. Theory, Cambridge, July 2012.